Pythagoras

Wetenschapper
Buste van Pythagoras
Persoonlijke info
Volledige naam	Pythagoras van Samos
Bijnaam
Pseudoniem
Geboren	ca. 570 v. Chr.
Geboorteplaats	Samos
Geboorteland	Griekenland, vlak bij Turkije
Overleden	ca. 495 v. Chr.
Overleden te	ofwel Croton of Metapontum, zuid-Italië
Gehuwd met / relatie	mogelijk met Theano, een dame van Kreta
Bekend van
Vakgebied	Ethiek, Wiskunde, Metafysica, Muziek-theorie, Mystiek, Politiek en Religie
Actief	Oud Grieks
Bekend van	Vijf klimaatzones, Vijf geometrische figuren, Proporties, de stelling van Pythagoras, Pythagoras stemming (soort toonladder), Bolvormigheid van de aarde, vegetarisme
Portaal Wetenschap

Pythagoras is geboren in Samos, ca. 570 v.Chr. en gestorven in Metapontum, ca. 500 v.Chr. Hij was een bekende Griekse filosoof,astronoom en wiskundige. Als filosoof richtte hij zijn eigen school op en onderwees de onsterfelijkheid van de ziel en reïncarnatie. Hij leerde ook dat alle dingen getallen waren en dat alles in het universum in harmonie was. Het beroemdst is hij door zijn wiskundige 'stelling', hoewel die waarschijnlijk pas later door zijn volgelingen, de pythagoreeërs, werd ontwikkeld.

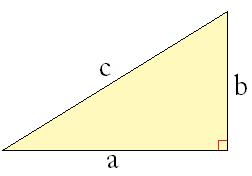
Hij heeft de stelling van Pythagoras bedacht. Hiermee kun je de zijden van een rechthoekige driehoek berekenen als je er al twee weet.

De formule is a²+b²=c².

(ook op te schrijven als r²+r²=s² met r=rechthoekszijde en s=schuine zijde).

Voorbeeld:

Stel: in deze rechthoek is zijde a=3 cm, zijde b=4 cm en zijde c=?

a²+b²=c², dus

3²+4²=c²

9+16=c²

9+16=25=c²

c=√25, dus c= 5 cm

Het bovenstaande voorbeeld geeft weer hoe we de schuine zijde c kunnen berekenen. We kunnen ook een beetje spelen met deze formule om zo een rechthoekszijde (zijde a of b) te berekenen.

Voorbeeld:

Stel: c = 10 cm en a = 8 cm. Welke lengte heeft b nu?

We gebruiken opnieuw de stelling van Pythagoras,

a²+b²=c²

maar verplaatsen nu a² naar de rechterkant:

b² = c² - a²

b² = 10² - 8² = 100-64

b² = 36

b=√36, dus b = 6 cm