Wortel (wiskunde)

Werk in uitvoering Aan dit artikel wordt de komende uren of dagen nog gewerkt. Belangrijk: Laat dit sjabloon niet langer staan dan nodig is, anders ontmoedig je anderen om het artikel te verbeteren. De maximale houdbaarheid van dit sjabloon is twee weken na de laatste bewerking aan het artikel. Kijk in de geschiedenis of je het artikel kunt bewerken zonder een bewerkingsconflict te veroorzaken.

Werk in uitvoering Aan dit artikel wordt nog hard gewerkt.

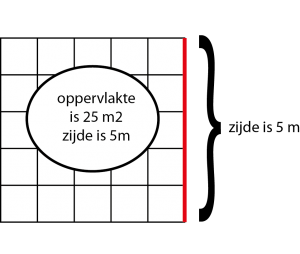
Een wortel is een getal. Het is een getal dat te maken heeft met de oppervlakte van een vierkant en de zijde van dat vierkant. Als je weet wat de oppervlakte is van een vierkant, dan is de wortel de lengte van de zijde van dat vierkant. Als de oppervlakte van een vierkant, bijvoorbeeld vijfentwintig is, dan is één zijde van dat vierkant vijf. Je zegt dan dat de wortel van vijfentwintig vijf is.
De wortel van vijfentwintig is vijf. Als je de tafel van vijf goed kent dan weet je dat vijf keer vijf vijfentwintig is. Vijf keer vijf noem je ook wel het kwadraat van vijf. In rekentaal ziet de wortel van vijfentwintig er zo uit:

<math>\sqrt[n]{a}</math>.

<<hier rekentaal invoegen>>

De wortel van 9 is 3. Want 3 × 3 = 9. Dus de wortel van 64 is 8, want 8 × 8 = 64. Het omgekeerde van de wortel is kwadraat. Het kwadraat van 3 is 9 en die van 8 is 64. Die doet precies het omgekeerde!