Bruggen van Koningsbergen (puzzel)
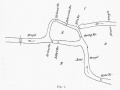
Een beroemde puzzel is het zogeheten probleem van de Bruggen van Koningsbergen. Door deze Duitse stad (tegenwoordig in Russisch bezit en herdoopt in Kaliningrad) loopt de rivier de Pregel. Tegenwoordig gaan de mensen er op hun vrije dag met de auto op uit, maar vroeger was het heel beschaafd een stukje te gaan wandelen. De enige vrije dag waarover de mensen vroeger beschikten, was de zondag. Vandaar de benaming "zondagmiddagwandeling". Dat deden ze in Koningsbergen ook. De eilandjes in de Pregel waren onderling en met de oever verbonden door zeven bruggen, zoals op tekening 1. De inwoners probeerden nu zo te wandelen, dat ze alle bruggen passeerden, maar elke brug hoogstens één keer. Maar wat ze ook deden, het lukte nooit. Ten einde raad vervoegden ze zich bij de wiskundige Euler. Die bewees, dat het onmogelijk was.
De oplossing van Euler
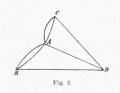
Eerst "vertaalde" Euler het probleem van de bruggen in een eenvoudiger vorm. Hij stelde elke oever en elk eiland voor door een punt op een stuk papier en elke brug door een lijn, die de punten verbond. De figuur, die ontstond, staat naast het kaartje (tekening 2). Toen luidde het probleem: de hele figuur te tekenen zonder één lijn tweemaal te trekken. Door een groot aantal verschillende figuren van dit type te bestuderen, kwam Euler er achter, welke lijnen op deze manier konden worden getrokken en welke niet.
Waarom de wandeling niet lukte
Zo waren er punten, waar een even aantal lijnen bij elkaar kwamen. Die noemde hij even knooppunten. En er waren punten, waar een oneven aantal lijnen bij elkaar kwamen. Deze punten noemde hij oneven knooppunten. Hij kwam er achter, dat het aantal oneven knooppunten in een figuur altijd even is. Daarop toonde hij aan dat je alleen een figuur kunt tekenen zonder het potlood op te lichten en zonder een lijn tweemaal te trekken, als het aantal oneven knooppunten in een figuur 2 of 0 is. Als de figuur meer dan twee oneven knooppunten telt, is het onmogelijk. De figuur van de bruggen in Koningsbergen telt 4 oneven knooppunten. Daarom lukte het de inwoners van Koningsbergen niet elke brug hoogstens eenmaal te passeren.
Als een figuur geen oneven knooppunten telt, kun je op elk willekeurig punt met tekenen beginnen en eindigen waar je begon. Als een figuur twee oneven knooppunten telt, moet je beginnen bij het ene oneven knooppunt en dan eindig je bij het andere.
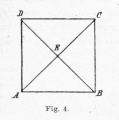
Van de twee hierbij ook afgebeelde figuren kan de linker (tekening 3) getekend worden zonder het potlood van het papier te lichten en een lijn tweemaal te trekken, terwijl dat bij de rechter (tekening 4) niet lukt. Of toch? Probeer het maar eens.