Platonische vormen: verschil tussen versies
| Regel 12: | Regel 12: | ||
De '''octaëder''' bestaat uit achtvlakken en wordt daarom ook achtvlak genoemd. Acht gelijkvormige driehoeken komen samen waarbij elk hoekpunt 4 driehoeken verbindt. Er zijn in totaal 6 hoekpunten. | De '''octaëder''' bestaat uit achtvlakken en wordt daarom ook achtvlak genoemd. Acht gelijkvormige driehoeken komen samen waarbij elk hoekpunt 4 driehoeken verbindt. Er zijn in totaal 6 hoekpunten. | ||
| − | De dodecaëder, ook wel twaalfvlak genoemd, bestaat uit 12 vijfhoeken. Op elk hoekpunt komen 3 vlakken samen. In totaal heeft deze vorm 20 hoekpunten. | + | De '''dodecaëder''', ook wel twaalfvlak genoemd, bestaat uit 12 vijfhoeken. Op elk hoekpunt komen 3 vlakken samen. In totaal heeft deze vorm 20 hoekpunten. |
| − | De icosaëder is een twintigvlak, opgebouwd uit 20 driehoeken. Op elk hoekpunt komen 5 vlakken samen. Er zijn in totaal 12 hoekpunten. | + | De '''icosaëder''' is een twintigvlak, opgebouwd uit 20 driehoeken. Op elk hoekpunt komen 5 vlakken samen. Er zijn in totaal 12 hoekpunten. |
[[Bestand:Tetrahedron.jpg|left|thumb|Tetraëder. Drie driehoeken komen samen op elk hoekpunt. De vorm bestaat uit 4 vlakken]] | [[Bestand:Tetrahedron.jpg|left|thumb|Tetraëder. Drie driehoeken komen samen op elk hoekpunt. De vorm bestaat uit 4 vlakken]] | ||
Versie van 26 feb 2017 01:01
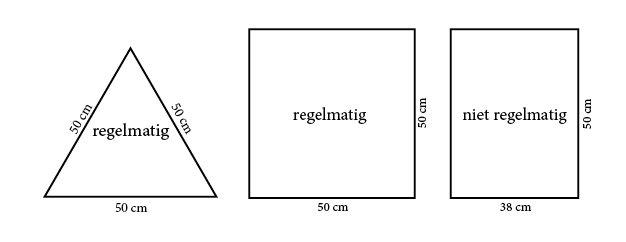
Een Platonische vorm, ook wel regelmatig veelvlak genoemd, is een driedimensionale vorm die bestaat uit regelmatige veelhoeken. Dat zijn bijvoorbeeld een driehoek of een vierkant.
Een regelmatige veelhoek heeft minimaal 3 hoeken waarvan de zijden allemaal even lang zijn. Een rechthoek heeft 2 zijden die korter zijn dan de andere 2 en is dus geen regelmatige veelhoek.
In totaal zijn er 5 Platonische vormen: tetraëder (tetrahedron), hexaëder (hexahedron), octaëder (octahedron), dodecaëder (dodecahedron) en icosaëder (icosahedron). De namen tussen de haakjes zijn de Griekse namen. De vormen zijn vernoemd naar Plato, een Griekse filosoof (denker) die leefde van 427 v. Chr - 347 v. Chr. Hij was de eerste die de regelmatige veelvlakken beschreef.
Vier platte driehoeken aan elkaar die op elke hoek met nog twee andere platte driehoeken samenkomen is een tetraëder. Het wordt ook een viervlak genoemd, omdat de vorm uit totaal 4 driehoeken bestaat.
Een hexaëder bestaat uit 6 vierkanten. Op elke hoekpunt van de vorm komen 4 vlakken samen. Dit wordt een hexaëder genoemd, of gewoon een kubus.
De octaëder bestaat uit achtvlakken en wordt daarom ook achtvlak genoemd. Acht gelijkvormige driehoeken komen samen waarbij elk hoekpunt 4 driehoeken verbindt. Er zijn in totaal 6 hoekpunten.
De dodecaëder, ook wel twaalfvlak genoemd, bestaat uit 12 vijfhoeken. Op elk hoekpunt komen 3 vlakken samen. In totaal heeft deze vorm 20 hoekpunten.
De icosaëder is een twintigvlak, opgebouwd uit 20 driehoeken. Op elk hoekpunt komen 5 vlakken samen. Er zijn in totaal 12 hoekpunten.




